Green communications are playing critical roles in vehicular ad hoc networks (VANETs), while the deployment of a power efficient VANET is quite challenging in practice. To add more greens into such kind of complicated and time-varying mobile network, we specifically investigate the throughput and transmission delay performances for real-time and delay sensitive services through a repeated game theoretic solution. This paper has employed Nash Equilibrium in the noncooperative game model and analyzes its efficiency. Simulation results have shown an obvious improvement on power efficiency through such efforts.
1. IntroductionWith the exponential growth of the energy consumption in wireless communications, Green communication has been drawing more and more attention in recent years [1–3]. It is reported that over 3% energy of global range is consumed by Information and Communication Technology (ICT), and such energy consumption will increase continuously in the future [4]. Transmission power, especially, has crucial impacts on enhancing the throughput of wireless communication. However, the unlimited extremely high transmission power is unable to improve throughput in many cases since it merely contributes to a terrible Signal-to-Interference-and-Noise Ratio (SINR) environment for each node. On the other hand, the energy consumption is also inefficient in a low SINR environment [5–8].
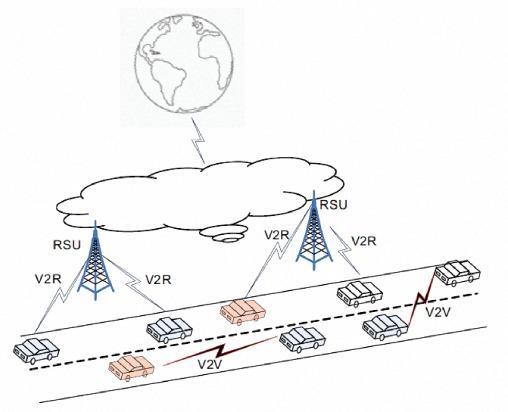
Power efficiency is becoming a major issue in vehicular ad hoc networks (VANETs), because of the consciousness of environment-friendly society [9, 10]. Unfortunately, the nature of VANETs is high mobility, and self-organized, leading to the power efficiency being ignored commonly. According to the structure of channel in VANETs, the control channel (CCH) allows nodes to disseminate packets with a fixed transmission rate [11]. The remaining six service channels (SCH) allow each node to choose the power level and modulation type to disseminate packets; it is possible to produce unpredictable interference. Moreover, due to the limitation of DSRC coverage range, it is difficult to extend the end-to-end service in a large and dynamic scale. Many experiments are performed based on the condition that each node is mandated to participate in the cooperation [10, 12]. As shown in Figure 1, the distance between the sender () and receiver () is outside of the coverage range of DSRC. To establish the link forand , the mandatory cooperation will certainly improve the receiving gain in VANETs. However, some nodes may not be suitable for such cooperation since they are suffering from severe communication environments. In Figure 1, some relay nodes (i.e.,and ) happen to be located on the marginal coverage of destination; the mandatory cooperation might cause the power efficiency to degrade over relay nodes. In this paper, we studied the basic composition of cooperation which is composed of packet forwarding [13]. We used packet forwarding strategy on each node as the entry point to discover the power efficiency in VANETs. A game theory model is proposed to analyze the behavior of each player (node and player are interchangeable in this paper) where each player has the objective to maximize its utility function. In the proposed noncooperative game, each node adjusts the power level and transmission rate through the packet forwarding strategy, achieving a balance between energy consumption and throughput based on current environment. Additionally, players know each other’s strategy set and payoff. Aforementioned characteristics are summarized as follows: (1) players are rational; (2) the player chooses their strategies independently; (3) complete information is shared. In the following system model section, we will discuss the Nash Equilibrium (NE) in the noncooperative game model and analyze its efficiency.
In this proposed scheme, we creatively deployed the VANETs by considering both node density and node mobility influences. Moreover, the proposed scheme is implemented by road side units (RSUs), since in VANETs RSUs often act as an Internet gateway and a centralized role to allocate channel resource [14].
The rest of the paper is structured as follows: Section 2 discusses the related work. Section 3 introduces system model and formulates the power efficiency game. In Section 4, we examine and analyze the experimental results based on VANETs environments. Finally, The conclusion of this paper is presented in Section 5.
Due to the development of ICT, the energy consumption andemission are becoming a major issue in academic and industry [2, 9, 10, 15]. In [16], the authors presented a directional routing and scheduling scheme, considering congestion, buffer, and delay for green VANETs. The paper [17] proposed an urban rescue operation based on VANETs. The target of this urban rescue operation is to reduce the energy consumption for green communication. Parameters to measure the green VANETs communication are throughput, time index in terms of travel time, and buffer time. On the other hand, to improve the bandwidth efficiency, [18, 19] introduced several channel coordination schemes for IEEE 802.11p/1609 vehicular networks. Additionally, in [6], authors proposed a scheme that applied a dynamic interval between the CCH and SCH. It showed that the proposed scheme enhanced saturation throughput based on IEEE 802.11p/1609 protocol. The impact of SINR is mentioned in [6, 7] where authors provide a model to evaluate the SINR for multichannel and multiusers environments. The papers [20, 21] proposed a basic framework based on game theory including some essential assumptions (i.e., the rational player).
Moreover, to describe the behavior of each node in a wireless ad hoc network, [20] proposed a noncooperative game model to analyze the effect of power level in the near-far model (NFE). The paper [21] also investigated the effect of power level based on game theory. The difference is [21] separate the system as several layers; then authors studied how an independent decision affects the performance of the network in the corresponding layer. The papers [13, 22] applied game theory to analyze the cooperation and packet forwarding mechanism in static wireless ad hoc networks. Especially, in [13, 23], authors pointed out that the interactions of nodes are different with different topology. They also determined which condition the cooperation and packet forwarding can exist without incentives. In [24, 25], authors studied a belief-based packet forwarding scheme. The paper [24] assumed a probability distribution function (PDF) to measure the belief on nodes. Then, nodes take action based on the result of PDF, and the belief function is updated by taking advantage of Bayes rule. Similar to [24], authors in [25] also proposed a belief-based scheme where the proposed method is to circumvent the complexity of calculating the belief function. The paper [26] designed the power control mechanism for the reputation-based scheme. The strategy set consists of the level of transmission power and the forwarding probability. In each round, nodes choose the energy consumption to send traffic; then nodes will update the forwarding probability based on the beliefs. In [27], authors studied an uplink power control environment where players are selfish to maximize its throughput under the power constraint scenario. They take both noncooperative and cooperative model under the power constraint scenario and provide the best response policy for the noncooperative game model. The paper [5] proposed an algorithm, combining the power consumption and transmission rate with the different SINR condition. The cooperation between nodes can be reached although the proposed algorithm is based on the noncooperative game model so that throughput will be improved in the network.
Many previous works have been done with the cooperation and packet forwarding strategies in wireless ad hoc networks. However, some previous works have to be modified due to the dynamic topology and mobility of nodes in VANETs.
3. System Model3.1. Part AWe first built a basic model in VANETs where the topology has a significant high mobility. A Poisson arrival process with the rate function is reputed as an appropriate traffic generation model ([28–31] in [32]). Following the assumption of Poisson arrival process, the average node density on the road is given by whererepresented a random velocity of the node which follows the Gaussian distribution.represented the probability of occurrence of each node.represented the Poisson with rate. Therefore, the average node number can be easily calculated by whererepresented the maximum communication distance. Following the Poisson arrival assumption, the distancebetween two adjacent nodes can be expressed in a pdf as follows: Correspondingly, the distancebetween two nonadjacent nodes will be the sum of (3), and it is expressed in the following pdf: whererepresented the number of nodes between the specified nonadjacent node andrepresented the node density. Then, based on the node density and the distance between nodes, we discussed the Bits Error Rate (BER) performance in VANETs. The interference between two nodes is reflected in the SINR [33]. whererepresented the destination node,represented the noise at the destination node,represented the path loss of the link from nodesto , andrepresented the power that node is using at this transmission time slot.
The channel fading between two nodes is supposed to follow the Rayleigh fading. The experimental vehicular channel measurement is used to estimate the path loss. A linear relationship between the path loss and the distance between senderand receiveris discussed by [34–36]. Therefore, this path loss model is simplified but very accurate; it is expressed as follows:represented a reference distance, normally choosing 1 meter.represented the path loss observed at the reference distance.represented the distance between two players,represented the path loss exponent, andis a random value following a normal distribution with zero mean.
Moreover, the throughput of a node in the game is expressed as follows:represented the data length.indicates the BER at the receiving node references to the average delay of the node. In VANETs, the Markov chain model in Figure 2 that Bianchi proposed in [37] has been widely used to estimate the delay of each node in VANETs. Since this paper does not focus on each node’s delay analysis, the conclusion in [37, 38] is quoted. whererepresented the packet that is supposed to be transferred in the network. Assume all the nodes in VANETs have the same probability to send the packet in one time slot (one time slot is equal to 100 ms in IEEE802.11p protocol [18, 19, 38]); it is easy to derivate that the increase of the nodes number will lead to the significant growth of traffic load. The average transmission time for one packetcan be expressed as follows (the proof of (9) is in the appendix part): whererepresented the duration that the channel is free (a free slot time is equal to 32 s).represented the duration of a transmission collision.represented the time needed to complete the payload transmission. It can be calculated by the data length divided by the data rate.represented the DIFS time in IEEE802.11p.represented the temporal cost of a successful transmission and it is expressed as follows: whererepresented the SIFS time in IEEE802.11p.represented the duration for transmitting one ACK pilot. Moreover, the probability of each transmission situation is also required to calculate thein (9). whererepresented the probability when the channel is idle.represented the number of nodes in the current environment.represented the stationary probability that nodes send the packet in the one-time slot.is the probability of a successful transmission anddenoted the probability that a channel collision occurs, as, so far, all the elements that will influence the delay performance in proposed game model are introduced.
3.2. Part BIn this part, we applied the aforementioned parameters in a noncooperative game model. The core idea of the game theory is to predict other players strategies and choose the best strategy depending on their utility. Nash Equilibrium as the most popular approach to predict which strategy to choose is wildly used. The mathematical definition of Nash Equilibrium is defined as follows.
Definition 1 (Nash Equilibrium). , if and only ifTheis called Nash Equilibrium.
Where theis denoted as player set,represented th player.represented the utility function for th.represented the th player’s strategy andrepresented the other player’s strategy. The Nash Equilibrium denotes that every player in the game choose a best response to each other’s strategy. In the other words, they can not enhance their utility except when other players change the strategy.
The different payoff function and cost function will contribute to the different Nash Equilibrium or even no Nash Equilibrium. Enumerating all the possibilities without practical assumptions will be confusing and inconclusive and therefore the detailed analysis will be presented in the simulation part combined with the realistic assumption in VANETs.
If Kakutani fixed point theorem is satisfied, at least one Nash Equilibrium will exist and all the rational players will choose the strategy that belongs to Nash Equilibrium. Otherwise, the player will choose the strategy based on the probability model since there is no Nash Equilibrium. After finding the Nash Equilibrium, Pareto Optimality and Social Optimality will be used to analyze the efficiency of the Nash Equilibrium.
Definition 2 (Pareto optimality). If and only if there is only one strategysatisfying and , the strategyis called Pareto-optimal (PO).
Definition 3 (social optimality). If and only ifwhererepresents the weight of th player, the strategyis called social optimal (SO).
PO is used to analyze the efficiency of each player. SO is used to analyze the efficiency of the entire network with the different weight of the players.
Moreover, one kind of dynamic game model repeated game is introduced to further improve the efficiency. Repeated game in game theory is often used to enhance the performance of the Nash Equilibrium by punishing the selfish node.
If players interacted by playing a similar stage game numerous times, this game is defined as a repeated game. As we mentioned earlier, the player set is denoted as .is a set denoted by the available strategies of th player in each round of the repeated game. We denotedas a set to record the action profile for each round andrepresented the player’s strategy in round .
In a repeated game, the historic utility function of a player will influence the current utility function of the player. Normally the effect of the round decay is made by adopting the exponential decay. The discount factor is , where ; when , the history of the player has no impact to the current utility. When , the history of player has the same impact as the current utility. The utility function of playerat roundcan be expressed as From the equation, it is easy to observe that the utility at roundwill decrease by a factor ofwhen estimating the utility of round . This factor can be used to model service which has the different priority. In VANETs back-off scheme, there are four different AC, which refer to the different QoS of the service. By giving the delay sensitive players small discount factor , and delay insensitive players big discount factor , the efficiency of Nash Equilibrium can be significantly increased by decreasing the loss of throughput.
The Power Efficiency Game (PEG) model is summarized in Table 1. We assumed all the players in this game are rational players, and every node tries to choose the strategies that can maximize the utility, where the functionsandrepresented throughput gain and energy consumption.
Components of a game Symbol Elements of VANETPlayers The set of decision-making nodes in the VANETsStrategy Actions set of node : Action of node :(reject forwarding)(participate forwarding) Joint action set: the Cartesian product of all , , Utility function The payoff function taking action The cost function taking action The utility function taking action :Consider the most fundamental game model, whereandas shown in Table 2, which denotes the fact that there are only two strategies that can be selected: forwarding the packet with powerand data rateor not forwarding the packet.
Player B Player A Strategy ForwardingNonforwarding (0) Forwarding Nonforwarding (0)The utility function of the player is the payoff function minus the cost function (a linear function) [5, 20, 21]. It is noteworthy that the interaction between two players needs to be considered. When two players transmit at the same time, we can use (5) to evaluate SINR for each node.
4. SimulationThis section complements the analysis of the different types of the game formulation mentioned in Section 3. At the same time, the optimal solution will be compared to find out the most suitable one according to the specific environment. In our simulation, we first showed the defect of mandatory cooperation based on the delay variation, and then we discussed the proposed game theory model where the player numberhas been set to 2. Without losing generality, the continuous power level has been chosen to be the strategy space. According to the standard of the IEEE 802.11p, maximum power is set to 760 mw. For V2V LOS environment, the path loss exponent equals 1.66, and the reference path loss at distance 1 m is set to 54.02. The link gain matrix assumes that all the drivers drive with good behavior, which means all the nodes keep the same speed with the front node when they are following; hence the Doppler shifting effect is considered as zero. The simulation has been completed in MATLAB based on the developing tool for power control game [4].
Considering the green communication, throughput itself is not appropriate to be the utility function. It is obvious that the throughput performance is better at a higher SINR. However, as we mentioned in Section 1, in some case, the mandatory cooperation will contribute to the degradation of throughput performance, since the delay and SINR will be violently affected. The simulation result in Figure 5 showed that the increase of average time delay is a nonlinear process with the increase of node number. The green line in Figure 3 is assumed to match the mandatory cooperation since the total transmitted packet is a random phenomenon and it is hard to approximate the certain number without knowledge experience. Relatively, the blue line is assumed to match packet forwarding without mandatory cooperation since at least one node existed that rejects to forward the packet or keeps silence. If nodes are allowed to choose the forwarding strategy by themselves, it is possible to approach blue line in the real world.
Meanwhile, in high SINR condition, the increase of the throughput performance can not catch up with the cost of the additional power. To improve the power efficiency of each player, the utility function is defined as the difference of throughput to power outlay. The simulation result in Figure 4 visualizes the discussion above; moreover, it finds the optimal SINR (5.7 dB) that leads to the highest utility. Hence the best response (BR) of all the players is 5.7 dB, and, based on that, a unique Nash Equilibrium (NE) exists when all the players choose the strategy that makes their SINR be 5.7 dB.
Adding cost function is the first optimal solution this paper discussed. The simulation result in Figure 5 finds the most suitable cost factor for the two-player power efficiency game. The green communication is concerned with the performance of the whole network, so the SO is selected as the criterion to evaluate the cost factor. The SO is evaluated by the sum of each player’s weighted utilitywhereis the weight of player . In our simulation, we assume all the players have the same priority; hence the SO utility is . From Figure 5, it shows that the SO achieves the maximum value 0.7621 when the cost factor is 0.141.
The simulation result in Figure 6 presents the efficiency of the Nash Equilibrium. The horizontal axis indicates player 1’s normalized utility and the vertical axis indicates player 2’s normalized utility. The best response to any player 1’s strategy is the gray area, and it is the same situation for player 2. Based on the definition of PO, the gray area is the PO region, and the solid curve is the PO frontier. The green cross mark represents the Nash Equilibrium of the two-player power efficiency game with cost factor equal to 0. The blue asterisk represents the enhanced Nash Equilibrium with the best cost factor (0.141). The solid circle represents the enhanced Nash Equilibrium of repeated power efficiency game. The red hollow square is the SO point, where the global best performance lies. As we observed from Figure 6, the simple Nash Equilibrium falls in the PO region which represents the fact that the Nash Equilibrium does enhance the power efficiency by making the players choose the best response to each other according to the optimal SINR. However, it still has some distance to the SO, which means that there is still some room to enhance the performance. The Nash Equilibrium with best cost factor (blue asterisk) is much closer to SO than simple Nash Equilibrium. Since the cost factor is a linear approach, it is hard to exactly reach the SO. Normally, there still will be some room to enhance the performance of Nash Equilibrium just as shown in Figure 6. Also, the Nash Equilibrium of repeated game (black solid circle) coincides with the SO. Normally, there still will be some room to enhance the performance of Nash Equilibrium just as shown in Figure 6. Also, the Nash Equilibrium of repeated game (black solid circle) coincides with SO, which indicates that the repeated game can provide the most efficient strategy in green communication.
It is also valuable to mention that, at the SO, the utility of player 2is bigger than the utility of player 1 . Because the link condition of player 2 is better than player 1, to get the global best performance, player 2 plays a more important role than player 1. It is extremely important when we discuss fairness problem in game theory to prevent the player from abandoning the game. In our assumption, it is avoided by forcing all the players to participate in the game. The point that the red line and the PO frontier crossed is that player 1 and player 2 have the same utility which means that all the players share the same fairness.
Without considering the fairness problem, the repeated game obviously has the best efficiency performance; however, all the players need to have the knowledge of all the previous strategies. The game with cost function has a good performance, but it needs an appropriate cost factor. According to different scenarios, the different optimal solution can be chosen.
5. ConclusionTo deploy a green vehicular ad hoc network under complicated and time-varying mobile environments, we specifically investigate the throughput and transmission delay performances for real-time and delay sensitive services through a repeated power efficiency game model. Nash Equilibrium was applied in the noncooperative game model, and its efficiency was analyzed based on IEEE 802.11p/1609 protocol. Simulation results have shown the repeated game, and the applied cost functions can provide the most efficient strategy in green communication. The future research work will be focused on the fairness problem and the various speed scenario.
AppendixOne has is the probability thattime slots exist between two successful transmissions.
is the expectation value of these time slots.
Since the probability of successful transmissionis less than 1 and larger than 0, the limit ofwhenapproach infinity can be expressed as follows:
The average time slot duration can be written as
Conflicts of InterestThe authors declare that there are no conflicts of interest regarding the publication of this paper.
