In game theory, repeated games, also known as supergames, are those that play out over and over for a period of time, and therefore are usually represented using the extensive form. As opposed to one-shot games, repeated games introduce a new series of incentives: the possibility of cooperating means that we may decide to compromise in order to carry on receiving a payoff over time, knowing that if we do not uphold our end of the deal, our opponent may decide not to either. Our offer of cooperation or our threat to cease cooperation has to be credible in order for our opponent to uphold their end of the bargain. Working out whether credibility is merited simply involves working out what weighs more: the payoff we stand to gain if we break our pact at any given moment and gain an exceptional, one off payoff, or continued cooperation with lower payoffs which may or may not add up to more over a given time. Therefore, each player must consider their opponent’s possible punishment strategies.
This means that the strategy space is greater than in any regular simultaneous or sequential game. Each player will determine their strategies or moves taking into account all previous moves up until that moment. Also, since each player will take into account this information, they will play the game based on the behaviour of the opponent, and therefore must consider also possible changes in the behaviour of the latter when making choices.
Repeated games provide different payoffs at each repetition, depending on each player’s moves. Since these payoffs are given at different points in time, in order to analyse repeated games, we must compare each player’s discounted sum of payoffs, which for infinite repetitions and finite repetitions are calculated using the following formulae:
Where: -P: the discounted sum of payoffs;
-t: the number of the repetition being considered;
-n: the total number of repetitions for finite repeated games;
-pt: the payoff at the repetition being considered;
-r: the discount rate.
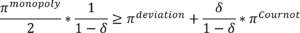
Repeated Prisoner’s dilemma:
In the game known as the Prisoner’s dilemma, the Nash equilibrium is Confess-Confess (defect-defect). In order to see what equilibrium will be reached in a repeated game of the prisoner’s dilemma, we must analyse two cases: the game is repeated a finite number of times, and the game is repeated an infinite number of times.
When the prisoners know the number of repetitions, it’s interesting to operate a backwards induction to solve the game. Consider the strategies of each player when they realise the next round is going to be the last. They behave as if it was a one-shot game, thus the Nash equilibrium applies, and the equilibrium would be confess-confess, just like in the one-time game. Now consider the game before the last. Since each player knows in the next, final round they are going to confess, there’s no advantage to lie (cooperate with each other) on this round either. The same logic applies for prior moves. Therefore, confess-confess is the Nash equilibrium for all rounds.
The situation with an infinite number of repetitions is different, since there will be no last round, a backwards induction reasoning does not work here. At each round, both prisoners reckon there will be another round and therefore there are always benefits arising form the cooperate (lie) strategy. However, prisoners must take into account punishment strategies, in case the other player confesses in any round.
Collusion agreement games:
If we assume the game can be played ad infinitum, we can apply it in a collusion agreement game, where two firms collude, forming a cartel. Consider two firms (a duopoly) that may either behave as Cournot duopolists earning profits πCournot each, or collude and act as a cartel, earning πCartel each, which correspond to the profits of a monopoly divided into the number of firms colluding (two in our example).
In this case, we simply need to apply the formula for calculating an infinite sequence and a discount factor to compensate for the fact that the gains to be derived are over time (accounting for impatience, inflation, loss of interest, etc.):
The left hand side represents the payoff derived from collusion, which can be held infinitely over time, with δ being the discount factor to bring future benefits forward to the present. For our threats or offers to be credible, this left hand side must be greater than the right hand side, which represents the one off payoff to be gained from deviating and breaking our cartel. The higher δ is, the higher the value assigned to future benefits and therefore the greater the chances of collusion. It is worth reminding here that fair competition is regulated in almost all countries, with cartels being banned, so most markets that lend themselves to reduced competition and price fixing are closely monitored.
Although this example is widely used in game theory and for the analysis of market structures, it can be easily seen that it does not represent a real situation. Let’s consider the same example: any of the colluding firms might deviate, in order to dump more output in the market at lower prices, in order to gain market share. This move will allow that firm to sell more products than the other firms, which directly contradicts Cournot’s premise that each duopolist will produce the same quantity. Therefore, considering a Stackelberg duopoly might seem more realistic. This would obviously change the analysis and outcome of the game.
